Grafische Ausgabe mit Python und Tkinter

Objekte und Grafiken (und erste Experimente)

In diesem und dem nächsten Kapitel erfahren wir die wichtigsten Grundlagen der objektorientierten Programmierung. Und wir bekommen erste grafische Ausgaben mit Hilfe von Python und Tkinter.

Die Butterfly-Kurve

Seit den glücklichen Zeiten mit meinem damals hochmodernen Atari ST habe ich die Schmetterlingskurve immer wieder als Test für die Grafikfähigkeit und Schnelligkeit von Programmiersprachen benutzt. Die Gleichung der Schmetterlingskurve sieht in Polarkoordinaten folgendermaßen aus:

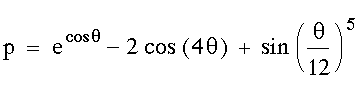
Die Gleichung ist hinreichend kompliziert um selbst in C geschriebene Routinen auf meinen damals unglaubliche 8 MegaBit schnellen Atari alt aussehen zu lassen. Rechenzeiten von 10 - 20 Minuten waren keine Seltenheit (einen Mac konnte ich mir damals nicht leisten). Und auf DOSen dachte man meisten noch gar nicht an Grafikfähigkeit: Windows kam gerade erst auf den Markt.

Zuerst einmal importieren wir die notwendigen Module:

#! /usr/local/bin/python    
#  Filename: butterfly.py
#  © 1999 by Jörg Kantel



import Tkinter
import Canvas
# für die Sinus- und Kosinus-Funktionen
import math
# für sys.exit(0)	
import sys		
from Tkconstants import *

Dann definieren wir uns eine Klasse Butterfly:

class Butterfly:
  def __init__(self, master = None):
    self.canvas = Tkinter.Canvas(master, relief = RIDGE, 
    bd = 2, bg = "white", width = 300, height = 300)
    self.canvas.pack()
		
  self.button = Tkinter.Button(master, text = " Run ", 
   command = self.draw)
  # Der Button soll nicht am unteren Rand "kleben",
  # daher werden oben undunten vier Pixel Rand angefügt.
  self.button.pack(side = BOTTOM, pady = 4)

Die Methode __init__ mit je zwei Unterstrichen vorne und hinten hat eine besondere Bedeutung. Sie wird immer dann ausgeführt, wenn eine neue Instanz der Klasse Butterfly erzeugt wird. In der Sprache der Objektorientierung wird eine solche Methode Konstruktor genannt.

Wir erzeugen in dieser Methode eine Zeichenfläche (in der Sprache von Tk ein Canvas und einen Knopf, dem wir das Kommande draw zuweisen. Mit self stellen wir per Konvention sicher, daß hier eine Methode der eigenen Klasse gemeint ist. (Dies entspricht dem this in Java oder C++.) Die Methode draw übernimmt das eigentliche Zeichnen auf der Zeichefläche und sieht folgendermaßen aus:

  def draw(self):
    theta  = 0.0
    while theta < 75.39:
      r = math.exp(math.cos(theta))-
        2*math.cos(4*theta)+(math.sin(theta/12))**5
     # aus Polarkoordinaten konvertieren:
      x = r*math.cos(theta)
      y = r*math.sin(theta)
      # auf Canvas-Größe skalieren
      xx = (x*30) + 150
      yy = (y*30) + 150
      if (theta == 0.0):
        Canvas.Line(self.canvas, xx, yy, xx, yy)
      else:
        Canvas.Line(self.canvas, xOld, yOld, xx, yy)
      self.canvas.update_idletasks()
      xOld = xx
      yOld = yy
      theta = theta + 0.02
    self.button.config(text = " Quit ",
    command = self.exit)

Es passiert eigentlich nichts aufregendes. In einer while-Schleife berechnen wir die Koordinaten unserer Funktion, rechnen die Polarkoordinaten in karthesiche Koordinaten um und skalieren das Ergebnis auf die Größe unserer Zeichenfläche. Neu sind nur die beiden Zeilen

self.canvas.update_idletasks()

und

self.button.config(text = " Quit ",
    command = self.exit)

In der ersten Anweisung erteilen wir Tk den Auftrag, nach jedem Zeichnen die Bildschirmasugabe zu aktualisieren. Wir können daher das Wachsen des Schmetterlings beobachten. Diese Anweisung verlangsamt allerdings die Berechnung erheblich. Sie können es selber ausprobieren. Wenn Sie diese Zeile auskommentieren, ist das Programm wesentlich schneller fertig. Dafür sehen Sie aber am Anfang aber auch nur auf eine leere Fläche und - schwupps - auf einmal ist der komplette Schmetterling da.

Die zweite Anweisung nutzt die Möglichkeit des Tk-Toolkits, Widgets zur Laufzeit zu verändern. In unserem Falle schreiben wir das Kommando »Quit« in den Button und ändern das Bindung an eine Methode auf die Methode self.exit. Dabei ist zu beachten, daß in Bindungen Methoden immer ohne Klammern geschrieben werden müssen. Die Methode selber ist einfach:

   def exit(self):
	    sys.exit(0)

Das ist unsere gesamte Klassendefinition. Der Rest des Programms ist wie gehabt: Wir erklären Tk zur Wurzel unseres Widget-Baumes, vergeben eine Titelzeile für unser Fenster und erzeugen eine Instanz der Klasse Butterfly. Und zum Schluß rufen wir die Hauptschleife von Tk auf:

if __name__ == "__main__":
   # Dies ist nur, damit der Titel angezeigt wird ;-)
   root = Tkinter.Tk()
   root.title("Butterfly Curve")
	
   # Erzeuge eine neue Instanz unserer
   # Schmetterlingsklasse ...
   butterfly = Butterfly(root)
   # ... und bringe sie zum Laufen.
   root.mainloop()

Und so sieht dann unser fertiges Programm aus:

Ist das nicht ein wunderschöner Schmetterling, den wir da mit nur ganz. wenigen Programmzeilen hingezaubert haben? Und schieben Sie ruhig auch einmal ein anderes Fenster über unser Schmetterlingsnest. Um das Neuzeichnen brauchen wir uns nicht zu kümmern, all dies erledigt Tk für uns.

Um die Formel verstehen zu können empfiehlt [WAGO93], nacheinander folgende Formeln plotten zu lassen:

in Polarkoordinaten
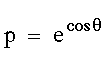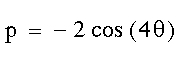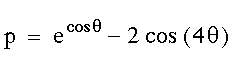in kartesichen Koordinaten
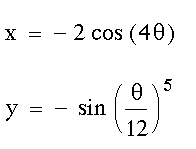in Polarkoordinaten

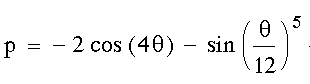Die Schmetterlingskurve und ähnliche Kurven wurden von Temple Fay an der Universität von Southern Mississpi entwickelt. Sie eignen sich vorzüglich zum Experimentieren. So weist [PICK92], S. 41ff. darauf hin, daß die Kurve

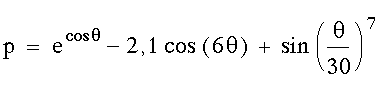
eine bedeutend größere Wiederholungsperiode aufweißt. Sie sind aufgefordert, auch damit zu experimentieren. Interessante Vergleiche mit der Originalschmetterlingskurve können Sie auch ziehen, wenn Sie mit

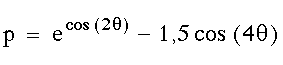
experiemtieren. Im Gegensatz zu meinen alten Atari sind heutige Rechner hinreichend schnell, so daß Sie auf die Ausgabe nicht ewig warten müssen. Und Python unterstützt sie durch seine Objektorientierung dabei, daß Sie den einmal geschriebenen Programmcode wiederverwerten können.

Literatur:

[FAY89]: Temple Fay: The Butterfly Curve, American Math. Monthly, 96(5); 442-443
[PICK92]: Clifford A. Pickover: Mit den Augen des Computers. Phantastische Welten aus dem Geist der Maschine, München (Markt & Technik) 1992
[WAGO93]; Stan Wagon: Mathematica^® in Aktion, Heidelberg (Spektrum Akademischer Verlag) 1993